|
sjm213
有小知識,無大學(xué)問。
級別: 論壇版主

   |
一、數(shù)制與碼制 1- 基本概念 不同的數(shù)碼可以用來表示數(shù)量的不同大小。用數(shù)碼表示數(shù)量大小時,僅用一位數(shù)碼往往不夠用,因此經(jīng)常需要用進(jìn)位計數(shù)制的方法組成多位數(shù)碼使用。 把多位數(shù)碼中每一位的構(gòu)成方法以及從低位到高位的進(jìn)位規(guī)則稱為數(shù)制。在數(shù)字電路中經(jīng)常使用的計數(shù)進(jìn)制有十進(jìn)制、二進(jìn)制和十六進(jìn)制。有時也用到八進(jìn)制。 不同的數(shù)碼不僅可以用來表示數(shù)量的不同大小,而且可以用來表示不同的事物或事物的不同狀態(tài)。在用于表示不同事物的情況下,這些數(shù)碼已經(jīng)不再具有表示數(shù)量大小的含義了,它們只是不同事物的代號而已。這些數(shù)碼稱為代碼。 為了便于記憶和查找,在編制代碼時總要遵循一定的規(guī)則,這些規(guī)則就稱為碼制。 2- 幾種常用的數(shù)制  4. 十六進(jìn)制數(shù)(Hexadecimal) 十六進(jìn)制數(shù)的進(jìn)位規(guī)則是“逢十六進(jìn)一” ,其進(jìn)位基數(shù)R=16,采用的16個數(shù)碼為0、 1、 2、…、 9、A、 B、 C、 D、 E、 F。 符號A~F分別代表十進(jìn)制數(shù)的10~15。每位的權(quán)是16的冪。 任何一個十六進(jìn)制數(shù), 可以表示為:  5. 不同進(jìn)制數(shù)的對照表 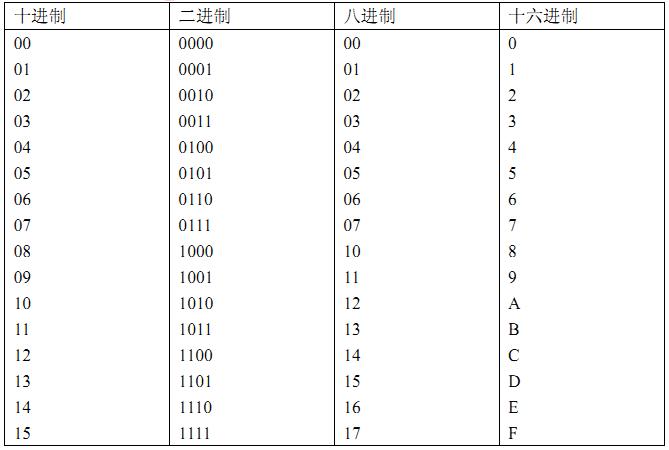 |
|---|---|
|
|
|
sjm213
有小知識,無大學(xué)問。
級別: 論壇版主

   |
3- 不同數(shù)制之間的轉(zhuǎn)換 1. 其它進(jìn)制轉(zhuǎn)換為十進(jìn)制 方法是:將其它進(jìn)制按權(quán)位展開,然后各項相加,就得到相應(yīng)的十進(jìn)制數(shù)。 例1: N=(10110.101)B=(?)D 按權(quán)展開N=1*24+0*23+1*22+1*21+0*20+1*2-1+0*2-2+1*2-3 =16+4+2+0.5+0.125 =(22.625)D 例2: N=(532.8)H=(?)D 按權(quán)展開N=5*162+3*161+2*160+8*16-1 =1280+48+2+0.5 =(1330.5)D 2. 將十進(jìn)制轉(zhuǎn)換成其它進(jìn)制 方法是:將十進(jìn)制數(shù)分整數(shù)部分和小數(shù)部分分別計算。 整數(shù)部分:(基數(shù)除法) 把我們要轉(zhuǎn)換的數(shù)除以新的進(jìn)制的基數(shù),把余數(shù)作為新進(jìn)制的最低位; 把上一次得的商在除以新的進(jìn)制基數(shù),把余數(shù)作為新進(jìn)制的次低位; 繼續(xù)上一步,直到最后的商為零,這時的余數(shù)就是新進(jìn)制的最高位。  注意:小數(shù)部分取整的過程,不一定能使最后乘積為0,因此轉(zhuǎn)換值存在誤差。通常在二進(jìn)制小數(shù)的精度已達(dá)到預(yù)定的要求時,運算便可結(jié)束。  3. 二進(jìn)制與八進(jìn)制、十六進(jìn)制之間的轉(zhuǎn)換 八進(jìn)制數(shù)和十六進(jìn)制數(shù)的基數(shù)分別為8=23,16=24, 所以三位二進(jìn)制數(shù)恰好相當(dāng)一位八進(jìn)制數(shù),四位二進(jìn)制數(shù)相當(dāng)一位十六進(jìn)制數(shù),它們之間的相互轉(zhuǎn)換是很方便的。 二進(jìn)制數(shù)轉(zhuǎn)換成八進(jìn)制數(shù)的方法是從小數(shù)點開始,分別向左、向右,將二進(jìn)制數(shù)按每三位一組分組(不足三位的補0),然后寫出每一組等值的八進(jìn)制數(shù)。 二進(jìn)制數(shù)轉(zhuǎn)換成十六進(jìn)制數(shù)的方法和二進(jìn)制數(shù)與八進(jìn)制數(shù)的轉(zhuǎn)換相似,從小數(shù)點開始分別向左、向右將二進(jìn)制數(shù)按每四位一組分組(不足四位補0),然后寫出每一組等值的十六進(jìn)制數(shù)。 例:  |
|---|---|
|
本帖最近評分記錄: |
|
sjm213
有小知識,無大學(xué)問。
級別: 論壇版主

   |
4- 二進(jìn)制算術(shù)運算 當(dāng)兩個數(shù)碼分別表示兩個數(shù)量大小時,它們可以進(jìn)行數(shù)量間的加、減、乘、除等運算。這種運算稱為算術(shù)運算。 因電腦和數(shù)字設(shè)備普遍采用二進(jìn)制運算,本節(jié)只探討二進(jìn)制的算術(shù)運算。 1. 二進(jìn)制算術(shù)運算的特點 二進(jìn)制算術(shù)運算和十進(jìn)制算術(shù)運算規(guī)則基本相同,區(qū)別是“逢二進(jìn)一”。  由上圖可見二進(jìn)制的乘法和除法有以下特點: 二進(jìn)制的乘法運算可以通過若干次的“被乘數(shù)(或0)左移1位”和“被乘數(shù)(或0)與部分積相加”這兩種操作完成; 二進(jìn)制數(shù)的除法運算能通過若干次的“除數(shù)右移1位”和“從被除數(shù)或余數(shù)中減去除數(shù)”這兩種操作完成。 如果我們能設(shè)法將減法操作轉(zhuǎn)化為某種形式的加法操作,那么加、減、乘、除運算就全部可以用"移位"和"相加"兩種操作實現(xiàn)了。為了解決這個問題,計算機引入了原碼、反碼和補碼的概念。 2. 原碼、反碼、補碼和補碼運算 二進(jìn)制數(shù)的正、負(fù)表示方法通常采用的是在二進(jìn)制數(shù)的前面增加一位符號位。這種形式的數(shù)稱為原碼。符號位為0表示這個數(shù)是正數(shù),符號位為1表示這個數(shù)是負(fù)數(shù)。其余各位表示數(shù)值。 在做減法運算時,如果兩個數(shù)是用原碼表示的,則首先需要比較兩數(shù)絕對值的大小,然后以絕對值大的一個作為被減數(shù)、絕對值小的一個作為減數(shù),求出差值,并以絕對值大的一個數(shù)的符號作為差值的符號。 這個操作過程比較麻煩,而且需要使用數(shù)值比較電路和減法運算電路。如果用兩數(shù)的補碼相加代替上述減法運算,則計算過程中就無需使用數(shù)值比較電路和減法運算電路了,從而使減法運算器的電路結(jié)構(gòu)大為簡化。 補碼的原理可參考其他電子書籍,正負(fù)數(shù)的反碼和補碼的計算原則如下: 反碼:正數(shù)的反碼等于原碼,負(fù)數(shù)的反碼:符號位不變,以下各位按位取反。 補碼:正數(shù)的補碼等于原碼,負(fù)數(shù)的補碼:符號位不變,以下各位按位取反,最后加1。一個數(shù)補碼的補碼即為其原碼。 例:帶符號位二進(jìn)制數(shù)00011010(+26)、10011010(-26)、00101101(+45)、和10101101(-45)的反碼和補碼。 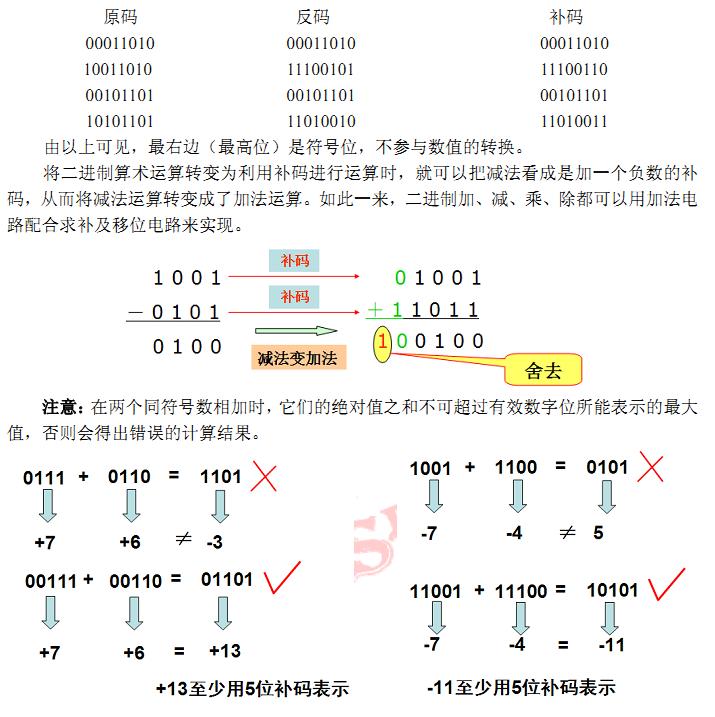 在計算機系統(tǒng)中,數(shù)值一律用補碼來表示(存儲)。 補碼的優(yōu)點主要有: 使符號位能與數(shù)值位部分一起參加運算,從而簡化運算規(guī)則; 使減法運算轉(zhuǎn)換為加法運算,從而簡化計算機中運算電路的設(shè)計; 兩個用補碼表示的數(shù)相加時,如果最高位(符號位)有進(jìn)位,則進(jìn)位被舍棄; 補碼轉(zhuǎn)換為對應(yīng)的十進(jìn)制數(shù)時正負(fù)數(shù)規(guī)則一樣 ; 0的補碼是唯一的。如0的5位補碼是00000。 |
|---|---|
|
|
|
sjm213
有小知識,無大學(xué)問。
級別: 論壇版主

   |
5- 幾種常見的編碼 1. 十進(jìn)制編碼 用四位二進(jìn)制碼的10 種組合表示十進(jìn)制數(shù)0~9,簡稱BCD碼(Binary Coded Decimal)。 這種編碼至少需要用四位二進(jìn)制碼元,而四位二進(jìn)制碼元可以有 16 種組合。當(dāng)用這些組合表示十進(jìn)制數(shù)0~9時, 有六種組合不用。由 16 種組合中選用 10 種組合。 8421BCD碼是最基本和最常用的BCD碼, 它和四位自然二進(jìn)制碼相似, 各位的權(quán)值為8、 4、 2、 1, 故稱為有權(quán)BCD碼。和四位自然二進(jìn)制碼不同的是, 它只選用了四位二進(jìn)制碼中前 10 組代碼,即用0000~1001分別代表它所對應(yīng)的十進(jìn)制數(shù), 余下的六組代碼不用。 下表為其他常用BCD碼,但在PLC中一般BCD碼僅指8421碼。 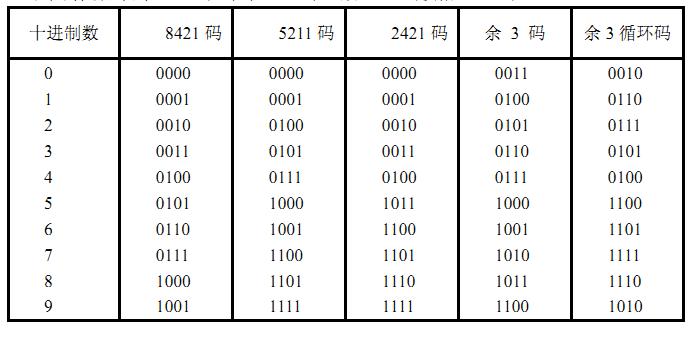 2. 格雷碼(Gray Code) 格雷碼又稱循環(huán)碼。每一位的狀態(tài)變化都按一定的順序循環(huán)。如果從0000開始,最右邊一位的狀態(tài)按0110順序循環(huán)變化,右邊第二位的狀態(tài)按00111100順序變化,右邊第三位按0000111111110000順序循環(huán)變化。 它的特點是:自右向左,每一位狀態(tài)狀態(tài)中連續(xù)的0、1數(shù)目增加一倍;編碼順序依次變化時,相鄰兩個代碼之間只有一位發(fā)生變化。 格雷碼消除了隨機取數(shù)時出現(xiàn)重大錯誤的可能,其反射和自補特性使得對其進(jìn)行求反操作也非常方便,所以,格雷碼屬于一種可靠性編碼,是一種錯誤最小化的編碼方式,因此格雷碼在通信和測量技術(shù)中得到廣泛應(yīng)用。工控行業(yè)中格雷碼的典型應(yīng)用是絕對值編碼器。 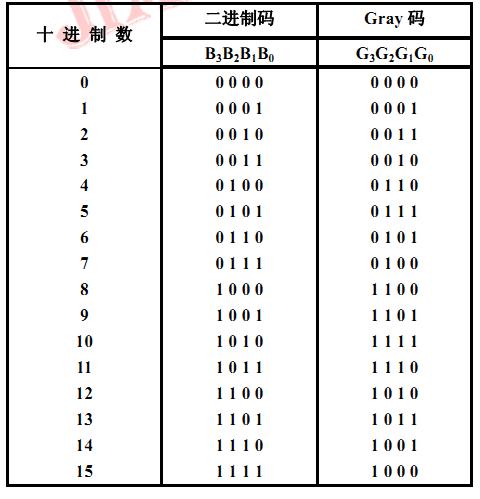 二進(jìn)制格雷碼(GRY)與自然二進(jìn)制碼(BIN)的互換: ①自然二進(jìn)制碼轉(zhuǎn)換成二進(jìn)制格雷碼 自然二進(jìn)制碼轉(zhuǎn)換成二進(jìn)制格雷碼,其法則是保留自然二進(jìn)制碼的最高位作為格雷碼的最高位,而次高位格雷碼為二進(jìn)制碼的高位與次高位相異或,而格雷碼其余各位與次高位的求法相類似。  3. 美國信息交換標(biāo)準(zhǔn)代碼(ASCⅡ) ASCII碼是一組7位二進(jìn)制代碼,主要用于表示各種字符。ASCII碼共128個,其中包括表示0~9的十個代碼,表示大、小英文字母的52個代碼,32個表示各種符號的代碼及34個控制碼。它可以用于通訊信息的傳輸和控制。 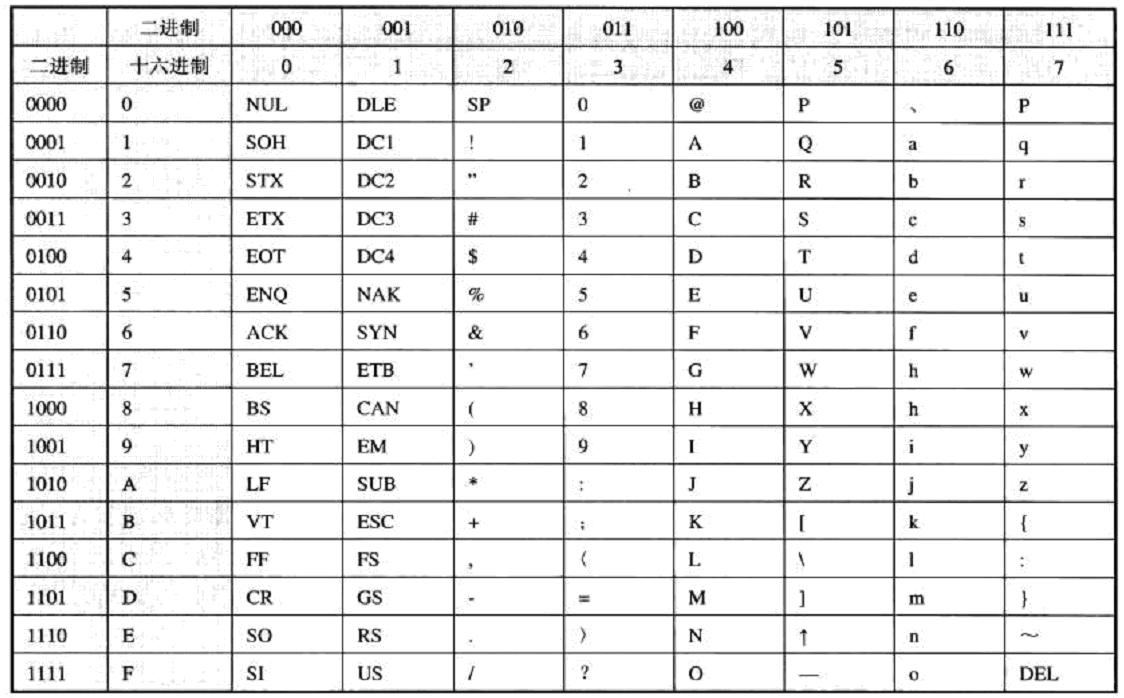 |
|---|---|
|
|
|
sjm213
有小知識,無大學(xué)問。
級別: 論壇版主

   |
這應(yīng)該用圖片傳上來,實際應(yīng)該是n次方,請注意: 例1: N=(10110.101)B=(?)D 按權(quán)展開N=1*24+0*23+1*22+1*21+0*20+1*2-1+0*2-2+1*2-3 =16+4+2+0.5+0.125 =(22.625)D 例2: N=(532.8)H=(?)D 按權(quán)展開N=5*162+3*161+2*160+8*16-1 =1280+48+2+0.5 =(1330.5)D |
|---|---|
|
|





 滬公網(wǎng)安備31010802001143號
滬公網(wǎng)安備31010802001143號